Brain-Twisters III
Pleae accept my apologies for failing to provide new puzzles during October and November. Research does tend to get in the way sometimes.
The puzzles in this page will generally be examples of the categories I enjoy most - those involving geometry, topology, probability, and truth paradoxes. Presenting them will often involve the use of tables and figures. The page should still be readable with text-based browsers such as Lynx, provided the reader has some way of downloading and viewing gif figures.
Puzzle #1
On his deathbed the Grand Vizier, who has two sons, announces that his entire fortune will go to the son whose horse loses a race in which the two of them must compete simultaneously. The sons, both keen horsemen, are accustomed to winning races but do not know how to lose them. Since in this case both are determined to lose, they do not see how such a race is possible, but a wise man explains how it can be managed. What simple method does he suggest?
Solution.
Puzzle #2
In his Last Will and Testament the Sheik says that anything not specifically bequeathed to a member of his family shall go to the Great Mosque. In the clause concerning his camels he makes the following provisions: "My eldest son will get half my camels, my middle son will get one-third, and my youngest son one-ninth."
Since there are seventeen camels, the sons do not know how to divide them without cutting one of the camels into pieces. While they are discussing the difficulty, a wise man (the very same sage from Puzzle #1) appears on a camel. The sons ask him what they should do. "Quite simple," he says. "Let us add my camel to yours. There are then eighteen camels, so the eldest of you will get nine, the second will get six, and the youngest two, which makes a total of seventeen, precisely the number that the Sheik left you." The sons divide the seventeen camels accordingly, and the wise man rides off on his own camel. Is this arrangement satisfactory from everyone's point of view? If not, why not?
Solution.
Puzzle #3
You are confronted with three bankers, one from Albania, one from America, and one from Austria. You do not know which is which, but you do know that one always tells the truth, a second always lies, and a third sometimes lies and sometimes tells the truth. How many questions are needed to identify their respective nationalities?
Solution.
Puzzle #4
What is the length of line x in the triangle drawn below?
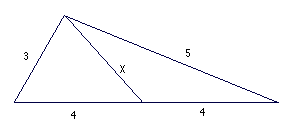
Solution.
Puzzle #5
Show, without using complicated quadratic equations and the like, that the area of the larger triangle is four times that of the smaller traingle in the figure drawn below.

Solution.
Visit:
Puzzles 1-3 adapted from Morris, I. (1970) The Lonely monk and Other Puzzles, Little, Brown & Co.
Puzzle 4-5 adapted from Gardner, M. (1981) Science Fiction Puzzle Tales, C. N. Potter.
Revised: November 30, 1996
