Brain-Twisters V
The puzzles in this page will generally be examples of the categories I enjoy most - those involving geometry, topology, probability, and truth paradoxes. Presenting them will often involve the use of tables and figures. The page should still be readable with text-based browsers such as Lynx, provided the reader has some way of downloading and viewing gif figures.
Puzzle #1
In a certain flower garden, each flower was either red, yellow, or blue, and all three colours were represented. A statistician once visited the garden and made the observation that whatever three flowers you picked, at least one of them was bound to be red. A second statistician visited the garden and made the observation that whatever three flowers you picked, at least one was bound to be yellow.
Two logic students heard about this and got into an argument. The first student said: "It therefore follows that whatever three flowers you pick, at least one is bound to be blue, doesn't it?" The second student said: "Of course not!"
Which student was right, and why?
Solution.
Puzzle #2
Suppose I offer to give you one of three prizes -- Prize A, Prize B, or Prize C. Prize A is the best of the three, Prize B is middling, and Prize C is the booby prize. You are to make a statement; if the statement is true, then I promise to award you either Prize A or Prize B, but if your statement is false, then you get Prize C -- the booby prize.
Of course it is easy for you to be sure to win either Prize A or Prize B; all you need say is: " Two plus two is four." But suppose you have your heart set on Prize A -- what statement could you make which would force me to give you Prize A?
Solution.
Puzzle #3
I now add a fourth prize -- Prize D. This prize is also a booby prize. The conditions now are that if you make a true statement, I promise to give you either Prize A or Prize B, but if you make a false statement, you get one of the two booby prizes -- Prize C or Prize D.
Suppose you happen to know in advance what the four prizes are, and for some reason or other, you like Prize C better than any of the other prizes. What statement could you make that would force me to give you Prize C?
Solution.
Puzzle #4
Messrs. Draper, Grocer, Baker, and Hatter are (appropriately enough) a draper, grocer, baker, and hatter. But none of them is the namesake of his own vacation.
When I tried to find out who is who, four statements were made to me:
(1) Mr. Draper is the hatter.
(2) Mr. Grocer is the draper.
(3) Mr. Baker is not the hatter.
(4) Mr. Hatter is not the baker.
But clearly there was something was wrong here, since Mr. Baker is not the baker. I subsequently discovered that three of the statements made to me were untrue.
Who is the grocer?
Solution.
Puzzle #5
The figure shows a small island, on which is a tree, in the middle of a large and deep lake, which is 300 yards across. On the shore is another tree.
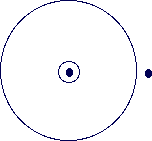
How might a man, who is unable to swim, with only a length of rope rather more than 300 yards long, get from the shore to the island?
Solution.
Visit:
Puzzles 1-3 adapted from Smullyan, R. (1982) To Mock a Mockingbird, Knopf.
Puzzle 4 adapted from Phillips, H. (1960) Problems Omnibus, Arco Publications.
Puzzle 5 adapted from Gardner, M. (1983) Wheels, Life and Other Mathematical Amusements, W. H. Freeman.
Revised: March 1, 1998
